skip to main |
skip to sidebar



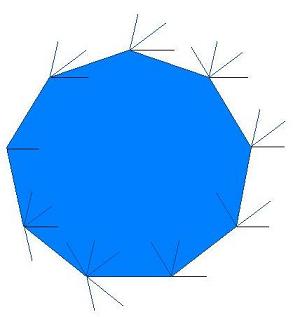

Xn = LCos (θ+ k ω) + Xn-1
Yn = LSen (θ+ k ω) + Yn-1


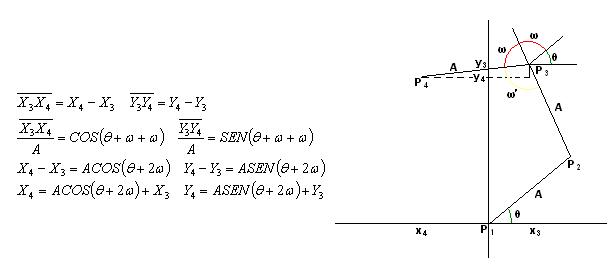


Para construir un polígono regular de n-lados se deben tener en cuenta:
Metodo Dabeja

BIOGRAFÍA:
Daniel Bejarano Segura, nació el 15 de septiembre de 1976 en la ciudad de Arauca, en el departamento de Arauca, bautizado en el municipio de San Juan de Arama en el departamento del Meta. Hijo de Juan Agustín “quién murió en 1982” y Sol Marina Segura Acuña quien tuvo que criarlos sola “cuatro hijos” radicados en la ciudad de Villavicencio, en el Barrio La Esperanza; realiza sus estudios de primaria en la concentración Fidel Agusto Rivera y a sus doce años entra al INEM “Luís López de Mesa” graduado en la promoción de 1993 en la modalidad Agropecuaria, en 1994 presta su servicio Militar Obligatorio obteniendo su libreta de primera clase, entra a la Universidad de los Llanos Orientales a la Licenciatura en Matemáticas y Física, donde se destacó por sus buenas calificaciones que le otorgaron Matrícula de Honor, siendo eximido de los derechos de grado, en el año 2000, en ese mismo año contrae matrimonio con Darkis Nelle Pérez Silva quien es Licenciada en Básica Con énfasis en Educación Artística, Viajan a la ciudad de Mitú en el departamento del Vaupés, donde son nombrados en propiedad en la Escuela Normal Superior Indígena Maria Reina “ENOSIMAR” Allí realiza trabajos de investigación desde las ciencias naturales “Física” “FENÓMENOS Y CREENCIAS NATIVAS 2002-2005” “CONCEPCIONES ETNICAS Y CIENTÍFICOS NATURALES 2004-2005” y la Etnomatemática “PENSANDO MATEMÁTICAMENTE DESDE NUESTRA CULTURA 2002-2006” reconocidos por el Ministerio de Educación Nacional quien los hizo partícipes del Foro Educativo Nacional en el 2003 por sus diversas experiencias significativas en el aula. Co-Autor del Libro “DIVERSIDAD CULTURAL EN LA FORMACIÓN DE MAESTROS, Universidad Pedagógica Nacional, Bogotá 2006 ediciones Géminis Ltda.” Capacitador de propuestas pedagógicas para la enseñanza-aprendizaje de las matemáticas “PENSAMIENTOS Y ESTRAGEGIAS EN EL ÁREA DE LAS MATEMÁTICAS” desde 2003 hasta el 2006. Reconocido por el departamento del Vaupés por sus innovaciones pedagógicas y administrativas, ese mismo año empieza a investigar sobre lo que hoy se denomina el Método DABEJA, en Junio del 2006 es trasladado de la ciudad de Mitú al Municipio de Vista Hermosa en la vereda de Piñalito en el departamento del Meta “antigua zona de distensión” y actualmente labora en la Institución Educativa IRACÁ Donde ha formado un semillero de investigación con estudiantes de grado décimo. Invitado al primer foro educativo municipal en Chía (Cundinamarca), luego representa al departamento del Meta en el Foro Educativo Nacional con el Método DABEJA, su investigación ha sido reconocida por las principales Universidades del País quienes lo han invitado a sus eventos en matemáticas como conferencista “XVIII ENCUENTRO DE GEOMETRÍA Y SUS APLICACIONES Y VI ENCUENTRO DE ARITMÉTICA BOGOTÁ,” “8º ENCUENTRO DE MATEMATICA EDUCATIVA, SANTIAGO DE CALI” XVI CONGRESO NACIONAL DE MATEMÁTICAS MEDELLÍN” entre otros , hoy en día continúa estudiando el comportamiento de figuras geométricas tratando de encontrar otras relaciones, que permitan comprobar la eficacia del método para cualquier figura plana y tridimensional.
INTRODUCCION
La geometría plana, que estudia las propiedades de superficies y figuras planas ha estado ligada desde sus inicios al compás como herramienta de graficación, los problemas de construcción, en los que cierta línea o figura debe ser construida utilizando sólo una regla de borde recto y un compás hacen parte en la enseñanza y aprendizaje de la geometría en los centros educativos desde hace tiempo, en especial los que no cuentan con computadores y otras tecnologías que faciliten este tipo de construcciones. El método DABEJA permite construir los polígonos regulares y las figuras planas sin emplear el compás, sólo a través de los puntos coordenados y ordenados en el plano cartesiano los cuales poseen una parametrización algebraica de las abscisas y ordenadas para cada figura, controlando las variables que entran en juego en la representación como el valor del lado, el del ángulo de rotación respecto de la horizontal y el ángulo externo encontrando reglas generales para la demostración matemática tipo geométrico y algebraico los cuales involucran conceptos trigonométricos básicos. En el transcurso del libro se encontrarán diversos capítulos que permiten al lector desglosar las figuras geométricas bidimensionales como los polígonos regulares en el primero, que generalizan dos fórmulas a nivel general que encuentran las abscisas y las ordenadas consecutivamente de los puntos o vértices de cada polígono regular, incentivando a la proyección de infinitos lados. Los diversos tipos de triángulos cada uno con su característica se ven en el capítulo dos, presentando el movimiento de un lado con respecto a otro siendo este mayor que el anterior, como un límite para entender las posibilidades que tiene un docente al querer construir un triángulo según sus ángulos. Los cuadriláteros continúan en el capítulo tres, identificando las diversas relaciones del cuadrado, rombo, romboide y rectángulo como por ejemplo todo cuadrado es un rectángulo pero no todo rectángulo es cuadrado, además los trapecios y trapezoides que ya han perdido su valor en cuanto a su enseñanza en la educación básica, nuevamente son caracterizados según sus partes internas y externas complementando su estudio. Otras figuras bidimensionales como las estrellas de n-puntas, el teorema de Pitágoras y el tangram, construidas a través del método DABEJA permiten encontrar las relaciones del movimiento que posee cada punto (vértice) respecto a sus ángulos y lados, estas relaciones se observan a simple inspección al determinar cada punto coordenado. Las transformaciones geométricas cuyas aplicaciones como las traslaciones, rotaciones o giros y homotecias hacen parte del capítulo cinco, reconociendo en ellas interacciones de los puntos coordenados y sus propiedades que los identifican sin tener en cuenta el tipo de figura que se desee mover. Se culmina con las construcciones de los cuerpos geométricos graficados desde el plano, recortadas y pegadas tipo plegados en dos dimensiones, las cuales desarrollan desde temprana edad la motricidad y la visualización espacial de estas construcciones que desarrolladas con valores reales, alcanzan tamaños jamás imaginados por los docentes de manera fácil y divertida para los estudiantes. El método DABEJA continúa encontrando otros aspectos geométricos de las figuras, siendo estos motivos de futuras investigaciones por parte de docentes y estudiantes con grandes aptitudes de investigación, permitiendo así un mayor desarrollo en las matemáticas y la labor docente en el aula.
CAPÍTULO 1.
FIGURAS GEOMETRICAS I
FIGURAS GEOMETRICAS I
1.1 POLIGONOS REGULARES:
1.1.1 Conceptos:
Figura plana cerrada constituida por n puntos (vértices) de los que en ningún caso pueden encontrarse alineados tres consecutivos (formando línea de 180º) y por n segmentos rectilíneos que unen entre sí a los vértices. “diccionario enciclopédico color. 2001” Todo polígono regular de n-lados tiene n-puntos coordenados y ordenados, P1(X1, Y1) P2(X2, Y2), P3(X3, Y3), P4(X4, Y4), P5(X5, Y5), Pn-2(Xn-2, Yn-2). Pn-1(Xn-1, Yn-1), Pn(Xn, Yn). Los cuales surgen por:
Yn = LSen (θ+ k ω) + Yn-1
Con LЄ R+, 0 ≤ θ ≤ 360º respecto a la horizontal K=n-2, n= puntos coordenados ω= (360/i), i= al número de lados. Donde L es el valor del lado que usted asigna y es cualquier número real, θ es el ángulo de rotación respecto de la horizontal, “asignado por usted” ω es el ángulo suplementario o externo y depende del número de lados del polígono, Xn y Yn “abscisas y ordenadas” puntos coordenados que generan los polígonos, Xn-1 y Yn-1 punto anterior respecto de Xn y Yn. “método DABEJA 2006”
1.1.2 Fórmulas método DABEJA para polígonos regulares y generalización.
Estas fórmulas contienen variables conocidas en cursos de trigonometría, como las funciones seno y coseno, ángulos de rotación “θ “, suplementarios “ω” e internos “ω´” puntos coordenados Pn= (xn, yn) cuyas componentes tiene valores reales positivos localizados en el plano cartesiano, el valor del lado del polígono regular “L”. Interactuando entre ellas para encontrar los puntos coordenados y ordenados que construyen la figura según sus lados.
FORMULAS PARA POLIGONOS REGULARES DE N-LADOS
| ||
X2 = LCos θ + X 2-1 |
X2 = LCos θ + X1 |
|
X3 = LCos (θ+ω) +X3-1 |
X3=LCos (θ+ω) + X2 |
|
X4=LCos (θ+2ω)+X4-1 |
X4=LCos (θ+2ω) + X3 |
|
X5 = LCos (θ+3ω)+X5-1 |
X5=LCos (θ+3ω) + X4 |
|
| ||
| ||
Y2 =LSen θ + Y2-1 |
Y2 =LSen θ + Y1 |
|
Y3 =LSen (θ+ω) + Y3-1 |
Y3 =LSen (θ+ω) + Y2 |
|
Y4 =LSen (θ+2ω) + Y4-1 |
Y4 =LSen (θ+2ω) +Y3 |
|
Y5 =LSen (θ+3ω) + Y5-1 |
Y5 =LSen (θ+3ω) +Y4 |
|
| ||
1.1.3 Demostración y Construcciones.
Se realizará la demostración y construcción del pentágono regular teniendo en cuenta los siguientes procesos apoyados en conceptos y relaciones trigonométricas, segmentos, ángulos y puntos coordenados.
En la construcción del pentágono regular se demuestra como los puntos coordenados y ordenados conservan el movimiento rotacional con ángulos de rotación “θ” y suplementarios “ω” cada vez que se encuentran sus coordenadas cartesianas ordenadamente. En la parte final de la demostración se comprueba que el punto final del pentágono regular es el mismo punto inicial, generando de manera cíclica los puntos coordenados posteriores limitándolo a encontrar tan solo cinco puntos coordenados y ordenados para construirlo. De manera similar se demuestran y construyen cada uno de los polígonos regulares de cualquier número de lados “se invita al lector a demostrar y construir el polígono regular que desee, apoyado en la fórmula general para polígonos de n-lados”
1.1.3 Construcción de Polígonos Regulares.
Para construir un polígono regular de n-lados se deben tener en cuenta:
- Los conceptos y variables mencionadas en apartados anteriores.
- El polígono es construido según los datos que usted plantee para las variables dadas.
- Manejar adecuadamente el plano cartesiano, la ubicación de puntos coordenados con valores reales positivos y su aproximación a decimales de una o varias cifras.
- Según el número de lados del polígono a construir así será el número de puntos a localizar.
- El ángulo suplementario para un polígono regular esta dado por ω = (360/i), donde i= al número de lados.
- Cada punto se une con el siguiente a través de un segmento de recta llamado lado del polígono.
- La rotación de la figura es respecto de la horizontal y toma valores de grados desde cero a trescientos sesenta, incluyendo minutos y segundos si lo desea.
- Después de encontrar todos los puntos del polígono, si usted, aumenta en uno el número de puntos se dará cuenta que es el punto inicial del mismo.
- Se recomienda emplear papel milimetrado.
Cabe recordar que los datos asignados son los que usted desee, dando el P1 punto inicial (x, y),
el valor del lado del polígono regular L= a cm. Con a Є R+, K=n-2, n= puntos
coordenados,
el ángulo de rotación de la figura 0 ≤ θ ≤ 360º y el ángulo externo
del polígono regular ω = (360/i),
i= al número de lados.
Cabe recordar que los datos asignados son los que usted desee, dando el P1 punto inicial (x, y), el valor del lado del polígono regular L= a cm. Con a Є R+, K=n-2, n= puntos coordenados, el ángulo de rotación de la figura 0 ≤ θ ≤ 360º y el ángulo externo del polígono regular ω = (360/i), i= al número de lados.
Si se desea construir un pentágono regular con:
|
|
|
|